Rotation - Maths

by bkenwright@xbdev.net

3D Graphics...its all maths... but its fun when you get past the basics.  One of the fundamental principles of 3D that you can't do without is Rotation of x,y,z points... either around the Z axis, Y-axis or even the X-axis...or all three...  But the reason people get lost is because of these nasty sin and cos things that pop up all over the place.... and then comes matrices...which make even the strongest of people at times cry!

But matrices isn't important... you can build a whole game without them....but you can't do a game without knowing how the maths of rotation works! 

With my great help, you'll have this theory stuff on rotation sorted!  ... Lets start with a sketch:

Now we start with a point...and for demonstration purposes, we'll rotate that point around the 'z' axis....so only the y and x values will change.  Our starting point will be Po...o is for old...and our new point which will have been rotated, will be Pn.... n is for new.

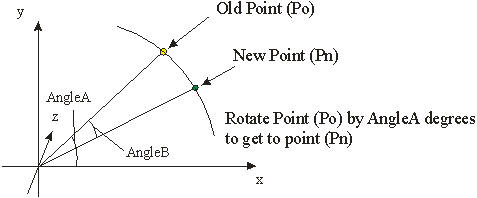
Here is where our trig comes into play!  Starting with point Po... its position can be found using simple trig...which is:

Po.x = r * cos (AngleA)

Po.y = r * sin (AngleA)

This is our Old Point...the point where starting at, and r is the radius of our point from the center, which of course is the same for both Po and Pn..... From Po, we are doing to rotate it by AngleB degree's to point (Pn)..... so if we take the angle of rotation and add it to AngleA...we get our new point Pn....giving us:

Pn.x = r * cos( AngleA + AngleB )

Pn.y = r * sin ( AngleA + AngleB )

But we don't really want to have to have AngleA hanging around...we just want to specify how much distance to rotate and rotate it by that amount!... But Trig Identities to the rescue.

As knowing:

sin(A+B) = sin(A) * cos(B) + cos(A) * sin(B)
cos(A+B) = cos(A) * cos(B) - sin(A) * sin(B)

Then substituting into our solution:

Pn.x = r * cos(AngleA)*cos(AngleB) - r *sin(AngleA)*sin(AngleB)

Pn.y = r * sin(AngleA)*cos(AngleB) + cos(AngleA)*sin(AngleB)

And using our magic...we know that

Po.x = r * cos (AngleA) and Po.y = r * sin (AngleA)... which we found earlier.... so we can substitute in....giving us:

Pn.x = Po.x * cos(AngleB) - Po.y * sin(AngleB)

Pn.y = Po.y * cos(AngleB) + Po.x * sin(AngleB)

And we can repeat the process for rotation about the y-axis and x-axis giving us the following equations:

Article of Reference:

ENTERING THE 3RD DIMENSION