|
Collision Detection Using Minkowski
Difference
by
Ben Kenwright
The
Minkowski Sum/Difference is a fast and relatively simple way of detecting whether two shapes interact. In
fact you might have already used it without realising it. In essence it works
by subtracting one object from another and then checking whether that new
object contains the origin. Of course its easier said than done subtracting one
object from another.
But we'll use basic shapes, such as spheres and cubes and use the technique
of support mapping.
In not so many words, support mapping, is where we take
a point inside an objects, for example the centre of mass. Then we project a ray outwards, now that ray
has got to hit a point on the surface of the shape, that point using
the ray from the centre is support mapping. Its easiest example is a sphere,
if you take the centre of the sphere and shoot a ray
out in any direction, you can easily work out point on the surface
of the ray.
 |
Using most shapes we can calculate the
support mapping ponit from a ray from its origin using relatively simple
maths. For example the simplest and easiest is the sphere.
Support mapping point is:
Support Point P = Radius * NormalRay.
Simple fire a ray in any
direction from our allocated centre and it returns the support
point on the surface.
So for each shape we can get
away with 2 simple functions. GetCentre() and GetSupportPoint( Vector3 normalFromCentre
).
|
To really push the theory home though we also have to do
a simple demo to show that you can actually use the support mapping to generate
the shapes surface.
|
Simple Demo  [60k SourceCode
& Executable ]
 [
Visual Studio 2008 with C#]
 [ XNA & Framework 3.1]
To try and show some examples of support mapping, I did a simple app
which generates some common
shapes (ellipsoid, sphere, cube, plane etc) using the support mapping technique.
Its very quick and dirty, but its
very effective in showing its workings.
Basically starts off with a shape around the origin, and then keeps firing a ray in
each direction till a tollerance has been
met. Using the points its aquired from firing the
ray it will build the shape triangles.
|
 |
This gives us a good starting point - we now have a
shape and a way of working out its surface point. This will help us create
a new shape using the Minkowski Difference.
One shape to Two....
Now we've got two shapes, and we can represent them both
by there support surfaces. So we need a reference centre for our new
shape. As long as its inside our new shape thats what matters. So a
good centre is the to the middle of both centre of masses of each object and do
the mean between them.
Vector3 v01 = q1.Rotate( p1.GetCentre() ) + t1;
Vector3 v02 = q2.Rotate( p2.GetCentre()) + t2;
Vector3 v0 = v02 - v01;
Subtracting the support points of one shape form another
and checking if the origin is inside the generated shape we can determine if our
two shapes have intersected.
o If A and B are intersection (i.e. Minkowski
Difference of A and B) then it contains the origin!
o The Minkowski Difference(A,B) = A.Support(n) -
B.Support(n) (i.e. just subtract one support point from another using the same
support normal)
Using some basic 3D math and the plane equation we can
loop around the shapes and check if there hitting.
 |
Demo: [ 69k Executable &
Source Code ]
Description: Move objects around using ASWD Keys
and to trigger shape changing colour when the objects intersect.
[Visual Studio 2008 with C#]
[ XNA & Framework 3.1]
The crosses are some of the test points that it
uses to generate the support difference of the 2 shapes before it finally
comes to the result of whether there is or isn't a collision. Not
you could force a full support manafold to build the actual shape
difference, but where interested in speed, and if we can determine in
advance if there is or isn't a collision we return the value and break
out. |
Intersection Information (Normals, Hit
Points, Penetration Depths)
Of course collision detection isn't really that useful,
unless you can gather extra information, such as the normal, the actual
collision points etc.
|
Demo: [ 48k Source
Code ]
Description: Move objects around using ASWD
Keys. When the objects intersect it will show the intersection point and the
normal with the shortest path to push the objects appart.
[Visual Studio 2008 with C#]
[ XNA & Framework 3.1]
|
|
Collision Manafold ("Contact
Manifold")
In a lot of physics systems that use collision detection,
in most cases the collision detection will return a single point which is the
point that is the furthest penetration and also a normal which is the direction
which is the shortest distance to take the shapes out of intersecting.
Of course if we have objects stacked or resting on each
other we can have multiple collisions. So what we end up doing is caching
the previous few collision points and updating them to determine if there still
valid, enabling us to build up a collision manifold which allows the shape to
settle down.
Keeping track of the manifold can be done in different
ways. One way which is popular and you'll find lots of information on the
net, is to use an Arbiter, which keeps track of which objects are intersecting
with with other object and keeps a list of the collision points. Then
using the collision points:
o Age
o Amount of movement from when it was created
o Number of collision points, first in, last out (old
ones get pushed out if we have to many)
o List Artbiters (ArbiterContainer)
o Arbiter - References 2 RigidBodies (uses
either id or pointer to identify which rigidboides)
- List contacts between the bodies
o Each frame we look for collisions between the
rigidbodies. If we have a collision we find the Arbiter between the 2
bodies. If one doesn't exist its added. Once we have the arbiter we
add the contact to it.
If no contacts exist, its a new contact and its just
added to the list of contacts. (ie. its position, normal, and
timestamp). Else if other contacts exist, check that its not withing some
threashold distance of it. e.g. 0.2 squared, if so, we will replace it
with the new collision point. This is done by replacing the collision
point and updating the contact normal and timestamp.
So when we add a new contact one of two things can
happen, its either a new contact or an existing contact is
updated.
| Code Snippet: Arbiter |
|
/*
We have a
single ArbiterContainer_c, which is just a static class array,
and stores a list of ArbiterItems
As new
points of contact between the pair are discovered, they are
added
to the
Arbiter with a call to AddContact().
*/
public
class ArbiterContainer_c
{
public class
ArbiterItem_c
{
public ArbiterItem_c(ArbiterKey_c key, Arbiter_c arbiter)
{
this.key
= key;
this.arbiter =
arbiter;
}
public ArbiterKey_c
key;
public Arbiter_c
arbiter;
};
public static
List<ArbiterItem_c> arbiterArray = new List<ArbiterItem_c>();
public static
Arbiter_c FindArbiter( ref RigidBody_c rb1, ref RigidBody_c rb2 )
{
ArbiterKey_c key = new ArbiterKey_c(ref rb1, ref
rb2);
for (int i=0; i<arbiterArray.Count;
i++)
{
if
(arbiterArray[i].key.b1.id==key.b1.id &&
arbiterArray[i].key.b2.id==key.b2.id)
{
return
arbiterArray[i].arbiter;
}
}
arbiterArray.Add( new ArbiterItem_c(key, new Arbiter_c(ref rb1, ref
rb2)) );
return arbiterArray[
arbiterArray.Count-1 ].arbiter;
}
static public
void DebugDraw(GraphicsDevice
graphicsDevice)
{
for (int i=0; i<arbiterArray.Count;
i++)
{
for (int k=0;
k<arbiterArray[i].arbiter.contacts.Count; k++)
{
Vector3 n =
arbiterArray[i].arbiter.contacts[k].normal;
Vector3 p =
arbiterArray[i].arbiter.contacts[k].point;
DrawLine_c.DrawLine(
graphicsDevice, p, p + n*10.0f, Microsoft.Xna.Framework.Graphics.Color.Yellow);
DrawLine_c.DrawCross(
graphicsDevice, p, 4.0f );
}
}
}
};
/*
Each
Arbiter maintains a list of contacts between two RigidBody
objects.
As new
points of contact between the pair are discovered, they are
added
to the
Arbiter with a call to AddContact().
*/
public
class Arbiter_c
{
public
Arbiter_c(ref RigidBody_c in1, ref RigidBody_c in2)
{
b1 = in1;
b2 = in2;
}
~Arbiter_c()
{
contacts.Clear();
}
public void
AddContact(Vector3 p1, Vector3 p2, Vector3 normal)
{
Vector3 point = (p1 + p2) *
0.5f;
int foundContact =
-1;
for (int i=0; i<contacts.Count;
i++)
{
if ((contacts[i].point -
point).LengthSquared() < 1.0f )
{
foundContact = i;
break;
}
}
if
(foundContact<0)
{
contacts.Add( new Contact_c(b1, b2, p1, p2, normal)
);
}
else
{
contacts[foundContact].point = point;
contacts[foundContact].Update( p1, p2, normal );
}
}
public RigidBody_c
b1;
public RigidBody_c
b2;
public List<Contact_c> contacts =
new List<Contact_c>();
};
/*
To find the
Arbiter for two RigidBodies, build an ArbiterKey for the two
bodies and
use it as the lookup key.
*/
public
class ArbiterKey_c
{
public ArbiterKey_c(ref RigidBody_c b1, ref RigidBody_c b2)
{
if ( b1.id < b2.id
)
{
this.b1 =
b1;
this.b2 =
b2;
}
else
{
this.b1 =
b2;
this.b2 =
b1;
}
}
public RigidBody_c
b1;
public RigidBody_c
b2;
}; |
|
|
Contact Manifolds Demo:
[ 55k Source
Code ]
Description: Move objects around using ASWD Keys
and to trigger shape changing colour when the objects intersect.
[Visual Studio 2008 with C#]
[ XNA & Framework 3.1]
Lets you add lots of test shapes and display various debug information
- using this technique of
caching the previous contact points, you can build up a contact
manifold so the shape settle. Cached contacts are updated and
removed as time progresses. |
So how many Cubes can we bounce around? Well with
un-optimised code and using C# we can probably get 50 cubes bouncing around
easily with realistic physics. Of course as you pass 100 you'll notice the
framerate really dropping, then you'll start to have to use some sort of world
partitioning for your collision detection (i.e BSP and Octree's). If your
running your code in C/C++ you can take advantage of optimising some of the
vector/matrix math to use SSE or maybe even just fast inline functions.
|
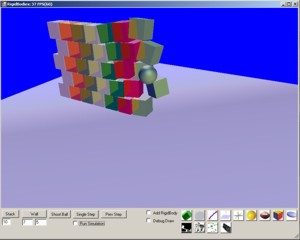
The screenshot shows 99 Blocks including the 5 walls which are also
blocks, you can run the demo and add in various other shapes, such as
balls, rugby's and tubes. You can add hundreds of shapes and you'll
get a stable simulation even though its frame rate drops
drastically. As long as you use a fixed time-step for your simulation
step.
If your running it for a game you can use a fixed time-step with a
catch-up loop to always maintain the same frame rate with the main game
loop.
|
|
Notes:
If your using the method for a physics system, you can
cache the collision points for dynamic contacts (Collisions) and using them for
numerous iterations for the collision response. But for the resting
contacts (static contacts) you'll find that you need to update the
collision data each iteration to solve the problem of jiggling. Its a bit
painful for performance but can be reduced if you use shock propagation for
stacking and spatial partitioning so only objects within vicinity of each other
need updating so its not so bad.s
Just for fun
Using the basic impulse physics principles, with a lot
more iterations so that the rigidbodies actually settled and didn't jiggle
around, I did a few samples that you can compile and run, ranging from
stacks of blocks (using shock propogation), dominos, bowling and a simple marble
slide. Feel free to fiddle around with it, its a good sample for the
collision detection code, letting you set forward/backwards frames to check
things and also debug draw the collision points etc.
 |
Fun Rigid Body Demo:
[ 69k Source
Code]
Adding various rigidbodies and showing there
various collisions with crosses. Also using simple impulses and to
make the samples more fun, I've done some simple test configurations -
dominos, sea-saws, walls, stack of blocks, marbles rolling down planks.s
[Visual Studio 2008 with C#]
[ XNA & Framework 3.1]
The sample sourcecode uses Seperated
Velocity/Position updates to improve stacking and reduce jiggling.
We also update the collisions and contacts seperately. And finally
we use a shock propogation technique for updating contacts so where able
to stack large numbers of rigidbodys. |
Various Sample Screenshots:
Theres a ton of different papers on collision detection
- its a fantastic subject and one which is constantly under research.
Either ways of speeding up existing algorithms, pushing them onto the gpu, or
modified hybrid versions. I'd definetly recomment do anyone if they had
time to do some reading on it.
Physics!...well again another juicy topic, lots of maths
and some very hard reading papers, but well worth it in the end when you see the
results you can get - from buildings flying appart when a ball hits it, or just
rain drops bouncing off the roof, theres endless things you can do...and you can
always simpliy the math so you have a add-hok version that gives you visually
pleasing results but isn't the full mathematical model. As most physics
simulations, especially realtime are making things as fast as possible and
looking as good as possible, even if you've got to cut a few corners.
References:
[Minkowski Collision Detection - JavaScript Version - Interact, Visualise and Understand]
https://xbdev.net/retro/code/collision-minkowski/index4.html
[Introduction to GJK]s
http://www.cas.mcmaster.ca/~carette/SE3GB3/2006/notes/gjk1_pres.pdf
[Contact Detection Algorithms]
http://www.academypublisher.com/jcp/vol04/no10/jcp041010531063.pdf
[Nonconvex Rigid Bodies with Stacking]
http://physbam.stanford.edu/~fedkiw/papers/stanford2003-01.pdfs
[XenoCollide]
http://xenocollide.snethen.com/
[WebGPU Minkowski Demo]
3D Interactive Code/WebGPU Minkowski
| 
