|
Rasterization : Drawing Lines
by
bkenwright@xbdev.net
When many people today start out in graphics they take things like Line
drawing algorithms for granted...or Triangle Fill API's etc in the DirectX
library's...with little or no understanding of how to implement a version
themselves. And as you can guess....that's what where going to do here
today. Where going to analyse how you'd draw a line to the
screen...taking into account optimisation and speed considerations.
Of course we'll still be using DirectX for the screen, so we can access the
screen pixels directly... but we'll be doing everything else ourselves.
A line, what is it? Well its two points... a source point...and a
destination point...
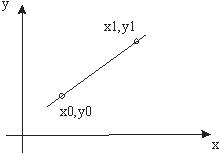
where y=mx +c is the equation of a line that where taught at school
Or alternatively put,
y = y0 + t*(y1-y0)
x = x0 + t*(x1-x0)
where t goes from 0 to 1 (usually represented as t => 0:1 )
But to the point...if we start at (x0,y0), then we can increment our changes
using the gradient... as show:
|
// int x0, y0 - start point
// int x1, y1 - end point
float dy = y1-y0;
float dx = x1-x0;
float m = dy/dx;
int y=y0;
for(int
x=x0; x<x1; x++)
{
y += m;
} |
That would be our simple approximation...and would work...
but there is one more thing in the world of computer code.... the y value of 0
is at the top of the screen...and increments downwards.
|
DownloadSourceCode |
|
void
Render(unsigned int*
pBits, int w, int
h, int pitch)
{
clearscreen(pBits, w, h, pitch);
int x0 = 100; //
start point
int y0 = 100;
int x1 = 200; //
end point
int y1 = 200;
float dy = y1-y0;
float dx = x1-x0;
float m = dy/dx;
float y=y0;
for(int
x=x0; x<x1; x++)
{
setpixel(pBits, w, h, pitch,
x,
(int)y,
0xffff0000);
y += m;
}
}//
End of Render(..) |
 |
So what we have is this...we increment x by 1 at a
time....and we increment y by the gradient m.....
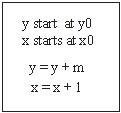
m = ( y1-y0) / (x1-x0)
Now the big big problem with the above code, which will be
mentioned in nearly every optimisation book, is the conversion of float to int....notice
the type casting in the setpixel(..) function call. As each time through
the loop we need to convert our float to a int to plot that pixel... now it may
not seem like much of a penatly ...but just you wait and see...when you start
rendering millions of triangles it soon slows down.
But there is a number of solutions... the first is an
approximation of the Bresenham Algorithm,... which uses the theory of how
we add fractions... as if you notice how we do this in our inner loop:
y += m
which is the same as:
y += dy/dx
or
y += (y1-y0)/(x1-x0)
If we note that when we add fractions, which the same
denominator...e.g. the same bottom divider amount...we only need to add the top
numerator values...and if it is greater than the denominator...we can just
subtract it... ..let me give you a simple example with numbers:
y = y + dy/dx
= y + dy/dx
y = y + dy/dx + dy/dx
= y + 2* dy/dx
y = y + dy/dx + dy/dx + dy/dx
= y + 3* dy/dx
Well I know I know..its a terrible example...I can only
hope you get a piece of paper out and dig the principle into your head...as
you'd be amazed how many times it pops up. So using this simple idea, we
can modify our line drawing algorithms
| DownloadSourceCode |
|
void
line(unsigned int*
pBits, int w, int
h, int pitch,
int x0,
int y0,
int x1,
int y1,
DWORD dwColour)
{
float dy = (float)y1-y0;
float dx = (float)x1-x0;
float m = dy/dx;
float ynum = dy;
float yden = dx;
int y = y0;
for(int
x=x0; x<x1; x++)
{
setpixel(pBits, w, h, pitch,
x, y, 0xffff0000);
ynum += dy;
if( ynum >= dx )
{
ynum -= dx;
y++;
}
}//
End for loop x
}//
End of line(..)
|
 |
But there is one more little thing which I've left out up
until now, as I didn't want to put to much information on you at once...its
whether you should increment x or y as the outer loop...if that makes any sense?
Let me give some examples as I try explain to those who are
new to this:
( dx > dy )
given: p0 = (2, 1) and p1 = (10, 2 )
...now dx = x1-x0 = 10 - 2 = 8
dy =
y1-y0 = 2 - 1 = 1
And our gradient m = dy/dx = 1/8
So if we increment x from x0 to x1 we go: 2, 3, 4, 5,
6, 7, 8... and we do the same for y... we get 1, 1.125, 1.25, 1.375... etc to 2.
But remember those decimal values are rounded off to integers...so we get
something like, 1,1,1,1, 2,2,2,2 for the y values :)
Well comes this next case:
(dy > dx)
say: p0=(2,1) and p1 = (3,6)
So we calcuate our dx and dy values, which come to:
dx = 1, dy = 5
Start x at x0, then increment it, and we have x1....which
is a single step...... 2, 3..... now do the same for y and we get 1,6 ...
ackkk...a jump from 1 to 6?... that can't look good....I'll show you a sketch of
what it looks like:
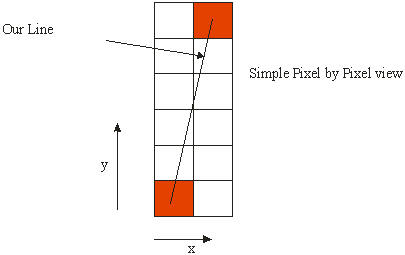
Well its better if you do a small sketch on a pad or
something... but the idea is, we determine to increment x or y in the outer loop
depending on whether dx or dy is largest.... and alter the gradient
appropriately...so our function code now becomes:
|
DownloadSourceCode |
|
void
line(unsigned int*
pBits, int w, int
h, int pitch,
int x0,
int y0,
int x1,
int y1,
DWORD dwColour)
{
float dy = (float)y1-y0;
float dx = (float)x1-x0;
float m = dy/dx;
if( dx > dy )
{
float ynum = dy;
int y = y0;
for(int
x=x0; x<x1; x++)
{
setpixel(pBits, w, h, pitch,
x, y, 0xffff0000);
ynum += dy;
if( ynum >= dx )
{
ynum -= dx;
y++;
}
}// End for loop x
}
else
{
float xnum = dx;
int x = x0;
for(int
y=y0; y<y1; y++)
{
setpixel(pBits, w, h, pitch,
x, y, 0xffff0000);
xnum += dx;
if( xnum >= dy )
{
xnum -= dy;
x++;
}
}// End for loop y
}
}//
End of line(..) |
 |
Well I guess it looks like a lot... but its really not that
much... you can probably see if better if I did it like this:
if( dx > dy )
x++;
y+=dy/dx;
else
y++
x+=dx/dy;
All that Besenham code makes things look messy and
complex...also I've layed it out in a simple to understand manner I hope...
The final straw, before moving on with our line algorithm,
is deciding if x0 is greater or less than x1..... as we can't rely on a person
using our line algorithm to use is by passing in the coordinates in a specific
order... so we must check for this and account for it! Always best to be
safe.
|
DownloadSourceCode |
|
void
line(unsigned int*
pBits, int w, int
h, int pitch,
int x0,
int y0,
int x1,
int y1,
DWORD dwColour)
{
int dy = y1-y0;
int dx = x1-x0;
int sdx = ( dx<0 ) ? -1 : 1 ;
// sign of dx and dy
int sdy = ( dy<0 ) ? -1 : 1 ;
dx
= dx * sdx;
dy
= dy * sdy;
int px = x0; //
starting point (x0,y0)
int py = y0;
if( dx > dy )
{
int y=0;
for(int
x=0; x<dx; x++)
{
setpixel(pBits, w, h, pitch,
px, py, 0xffff0000);
y += dy;
if( y >= dx )
{
y -= dx;
py += sdy;
}
px += sdx;
}// End for loop x
}
else
{
int x=0;
for(int
y=0; y<dy; y++)
{
setpixel(pBits, w, h, pitch,
px, py, 0xffff0000);
x += dx;
if( x >= dy )
{
x -= dy;
px+= sdx;
}
py+= sdy;
}// End for loop y
}
}//
End of line(..) |
 |
Well thats a pretty good method of drawing a line I
think... but there's more than one way to skin a cat as they say. When I
first learned that method, I thought it was the best...but with a bit of
creativity, you can do a line drawing algorithm using 'Fixed Point Maths'
It takes a bit of getting used to at first, but you'll soon
come around believe me....
So taking an approximation of our line drawing algorithm
using real numbers, it would be:
if( dx > dy )
{
for(x=0; x<dx; x++)
{
setpixel(px, py, colour)
px += sdx;
py += dy/dx;
}
}
else
{
for(y=0; y<dy; y++)
{
setpixel(px, py, colour)
py += sdy;
px += dx/dy;
}
}
|
Let me see....hmmm....a popular Fixed Point value is
16:16...where 16 bit's are for the whole number part, and 16 bits for the
decimal part....giving us:
#define FIXEDPOINT_16_16 16
So to convert a integer to a fixed point value we do this:
int iFPV = i << FIXEDPOINT_16_16;
Where iFPV is our new fixed point value.... So I re-wrote
our line drawing algorithm to use fixed point numbers....if you get
stuck...don't worry...just try some simple examples....things like this:
a = 10;
b = 33;
A = a << FIXEDPOINT_16_16; // Convert to fixed point
integer
B = b << FIXEDPOINT_16_16;
C = A+B;
c = C >> FIXEDPOINT_16_16; // Convert back to
standard integer
Few things to watch out for, when playing around with fixed
point numbers, is sign...as the upper most number with signed integers is used
to represent the sign of our value...so don't go converting negative values to
Fixed Point values without care...as it will give some crazy results.
| DownloadSourceCode |
|
void
line(unsigned int*
pBits, int w, int
h, int pitch,
int x0,
int y0,
int x1,
int y1,
DWORD dwColour)
{
int dy = (y1-y0);
int dx = (x1-x0);
int sdx = ( dx<0 ) ? -1 : 1 ;
// sign of dx and dy
int sdy = ( dy<0 ) ? -1 : 1 ;
dx
= dx * sdx;
dy
= dy * sdy;
int px = x0 << FIXEDPOINT_16_16;
// starting point (x0,y0)
int py = y0 << FIXEDPOINT_16_16;
// Should check for divide by zero errors here.
int dxdy = 0;
if( dy!=0 ) dxdy = ((dx <<
FIXEDPOINT_16_16)/dy)*sdx;
int dydx = 0;
if( dx!=0 ) dydx = ((dy <<
FIXEDPOINT_16_16)/dx)*sdy;
sdx
= (1 << FIXEDPOINT_16_16)*sdx;
sdy
= (1 << FIXEDPOINT_16_16)*sdy;
if( dx > dy )
{
for(int
x=0; x<dx; x++)
{
setpixel(pBits, w, h, pitch,
px>>FIXEDPOINT_16_16,
py>>FIXEDPOINT_16_16, dwColour);
py += dydx;
px += sdx;
}// End for loop x
}
else
{
for(int
y=0; y<dy; y++)
{
setpixel(pBits, w, h, pitch,
px>>FIXEDPOINT_16_16,
py>>FIXEDPOINT_16_16, dwColour);
px += dxdy;
py += sdy;
}// End for loop y
}
}//
End of line(..) |
 |
I know ...I know....thats a lot of code...and it looks
messy!....eekkKKkk... The algorithm has reached a peak in performance I think...
I didn't want you to think that you had done all this work and not got anything
to show for it, so I started up VTune from intel, which gives some performance
details ... and it showed quite a difference.
For the Beszenier Line algorithm (code_4), it was an
average of 1,567 clock cycles for the function....for our new improved fixed
point one, it came out to be 307! Wow!.. thats not bad...well I thought it
was okay.
We could make the SetPixel(..) function inline as well...to
make it a bit better I guess.... but why the performance difference was so
great? Well putting anything in a loop is bad! And those if
statements cost a lot more than a simple binary shift...as a simple example was
"if(y>=dx)" was cosing 145 clock cycles approx....
A careful think to look out for is simple "overflow" or
"out by one errors" when your developing or changing the code...its well worth
single stepping through it and checking the values :)
|